Stata夏令营是由北京友万信息科技有限公司主办，专为数据分析爱好者及专业人士打造的学术性实践活动，夏令营以Stata中国用户大会为依托，自2018年至今，已成功开展了七届。在每一届的夏令营活动中，参与者不仅可以深入学习和掌握Stata这一强大的统计分析软件，还能通过一系列精心设计的课程和实践活动，提升数据处理、统计分析及数据可视化的能力。Stata夏令营不仅是一个学习平台，更是一个充满活力和创意的交流空间。在这里，你可以结识来自不同领域的志同道合的朋友，共同探索数据分析的无限可能。无论你是初学者还是有一定经验的数据分析师，都能在Stata夏令营中找到属于自己的成长之路。我们诚挚邀请对数据分析感兴趣的你加入我们的行列，一起度过一个充实而难忘的Stata夏令营之旅！
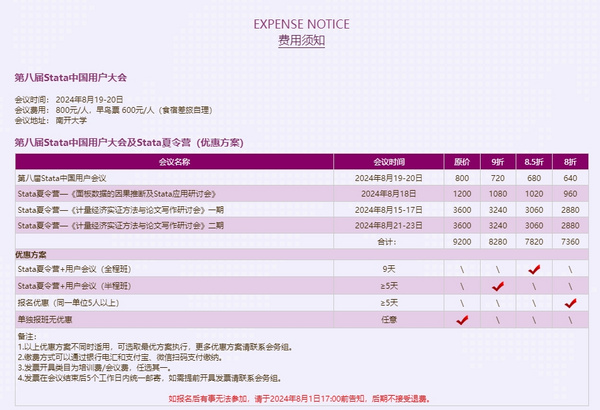
Stata夏季训练营暨《面板数据的因果推断及Stata应用研讨会》将于2024年8月18日在南开大学举办。即日起开始正式报名，欢迎广大Stata用户积极参与!
本次研讨会涵盖了区域政策研究的四种重要方法：比较案例分析、合成控制法、回归控制法和分位数控制法。比较案例分析作为传统方法，在案例选择上存在主观性。而合成控制法则通过客观方式选择控制组及权重，提高了分析的准确性。回归控制法无需协变量，利用信息准则或拉索估计量选择控制组，应用场景广泛。zui新的分位数控制法结合了机器学习方法，通过非参数分位数回归构造处理效应的置信区间，适用于异方差、自相关或模型误设的情况，尤其在小样本中表现出色。这些方法的介绍和案例分析，为区域政策研究提供了多元化的工具和方法，有助于更准确地评估政策效果。
陈强，山东大学经济学院教授，数量经济学博士生导师，研究领域为计量经济学、机器学习与经济史。分别于1992年、1995年获北京大学经济学学士、硕士学位，后留校任教。2007年获美国 Northern Illinois University 数学硕士与经济学博士学位。2010年入选教育部新世纪优秀人才支持计划。2017-2018年为 Boston College 访问学者，并在 Harvard, MIT 与 Boston University 旁听相关课程。已发表论文于Journal of Econometrics, Oxford Economic Papers (Lead Article), Journal of Comparative Economics, Economica, Stata Journal以及《经济学（季刊）》、《世界经济》等国内外领先期刊，并著有畅销教材《计量经济学及Stata应用》，《高级计量经济学及Stata应用》，《机器学习及R应用》与《机器学习及Python应用》。
课程概要
使用面板数据进行实证分析的一种常见情形式，处理组仅有一位或几位个体(地区)，而处理前的时期较多。此时，可使用合成控制法、回归控制法或分位数控制法进行有效的因果推断。其中，合成控制法zui为流行(Abadie and Gardeazabal, 2003; Abadie et al., 2010, 2015)，但需要协变量；而回归控制法则无须协变量，且算法简便(Hsiao et al., 2012)。然而，合成控制法与回归控制法主要依赖于安慰剂检验进行统计推断，在应用中有一定局限性。分位数控制法使用“分位数随机森林”(quantile random forest)的机器学习方法，通过非参数的分位数回归构造处理效应的稳健置信区间，在小样本中表现优异(Chen et al., 2024)。本课程将深入浅出地介绍合成控制法、回归控制法或分位数控制法，并通过经典案例演示相应的Stata操作。
学习要点
合成控制法、回归控制法或分位数控制法，以及Stata操作
课程对象
经管及社科类教师与研究人员、博士生、硕士生、高年级本科生。
课程配套资料
课程PPT、数据集、do文档及相关论文。
第1讲
比较案例分析
比较案例分析是区域政策研究的传统方法，可对少数案例进行深入分析，广泛应用于社会科学，但控制组的选择比较主观。
★ 案例：
马里矣尔船运(Mariel boatlift)对迈阿密劳动力市场的影响(Card, 1990)。
第二讲
合成控制法
合成控制法由比较案例分析发展而来，可以更客观而有效地选择控制组及权重。本讲介绍合成控制法的原理与算法、权重的稀疏性、时间安慰剂检验、空间安慰剂检验、混合安慰剂检验，以及留一稳健性检验。
★ 案例：
西班牙巴斯克地区恐怖活动的经济效应(Abadie and Gardeazabal, 2003)；
加州控烟法的效应(Abadie et al., 2010)；
德国统一的经济效应(Abadie et al., 2015)
第三讲
回归控制法
回归控制法的应用场景与合成控制法相同，但前者无须协变量，可使用信息准则或拉索估计量(Lasso)选择控制组。本讲介绍回归控制法的原理与算法，时间安慰剂检验、空间安慰剂检验，混合安慰剂检验，以及含协变量的回归控制法(Hsiao and Zhou, 2019)。
★ 案例：
香港回归以及与中国内地经济整合的效应(Hsiao et al., 2012)；
四万亿经济刺激政策的效应(Ouyang and Peng, 2015)；
上海与重庆房产税试点的效应(Du and Zhang, 2015)；高铁开通的政策效应(Ke et al., 2017)；
房票政策的房价效应(方诚、陈强, 2021)。
第四讲
分位数控制法
分位数控制法使用分位数随机森林的机器学习方法，通过非参数的分位数回归构造处理效应的稳健置信区间，在异方差、自相关或模型误设情况下依然有效，且在小样本中表现优异(Chen et al., 2024)。本讲介绍分位数控制法的原理与算法，包括决策树、随机森林与分位数回归森林。
★ 案例：
香港回归以及与中国内地经济一体化的效应(Hsiao et al., 2012)；
瑞典碳税对于二氧化碳排放的效应(Andersson, 2019)。
